M² and High-order Modes
M Squared | April 27, 2016
Introduction
M² is a measurement that was originally designed to determine the quality of a real beam in comparison to a theoretically perfect fundamental mode Gaussian beam (Siegman 1990). Although many lasers are designed to output a fundamental mode Gaussian beam, imperfections and/or cavity design in the laser will often cause superimposed higher-order transverse modes. M² provides an excellent metric for determining the higher-order mode content. In his original paper introducing M², Siegman gives mathematical expressions for the theoretical value of M² based on the weighted content of the various modes in a beam. In this blog post, we will programmatically generate Gaussian beams with multi-mode content and then analyze the M² value of these artificial beams calculated by the DataRay software in order to confirm the accuracy of our algorithms.
Higher-order Transverse Modes
The Hermite-Gaussian modes are found by solving the wave equation in Cartesian coordinates. The modes derive their name from the two instances of the Hermite polynomial in the equation for the modes’ electric field. The two Hermite polynomials are defined by their respective degrees, n and m, so that the overall mode is written TEMnm —where TEM\(_{00}\) is the fundamental mode.
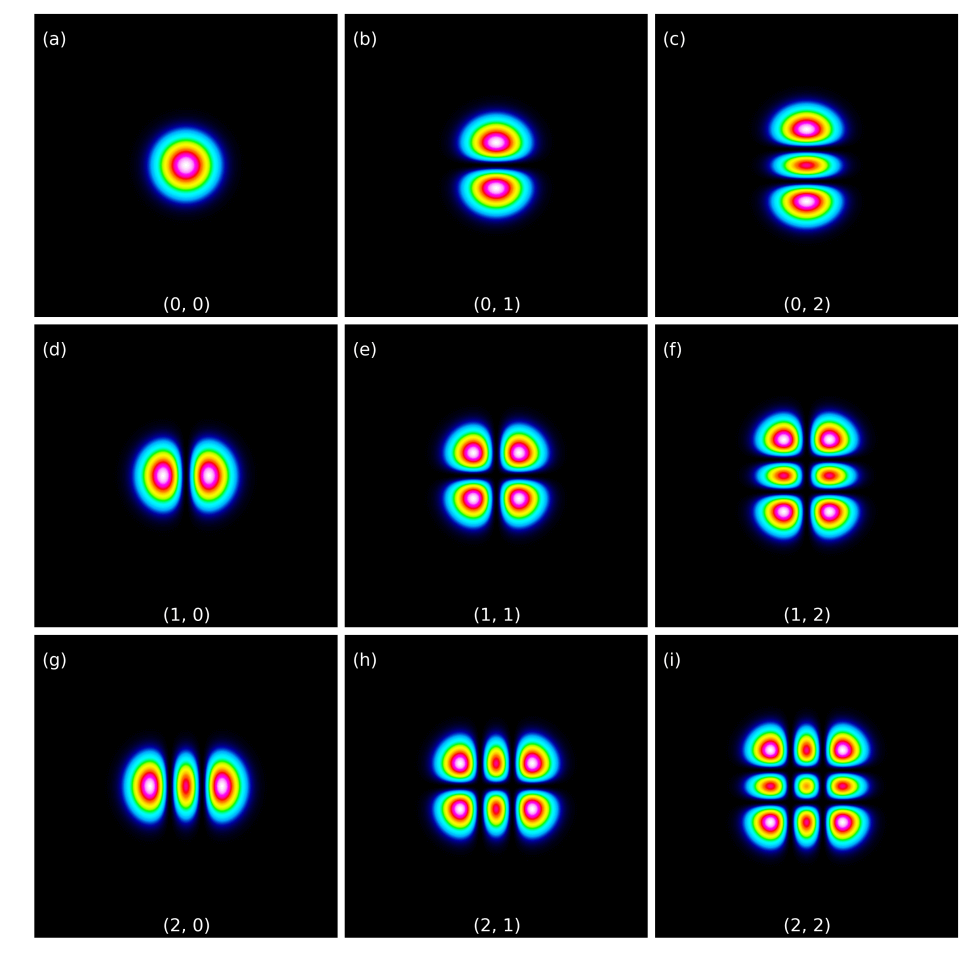
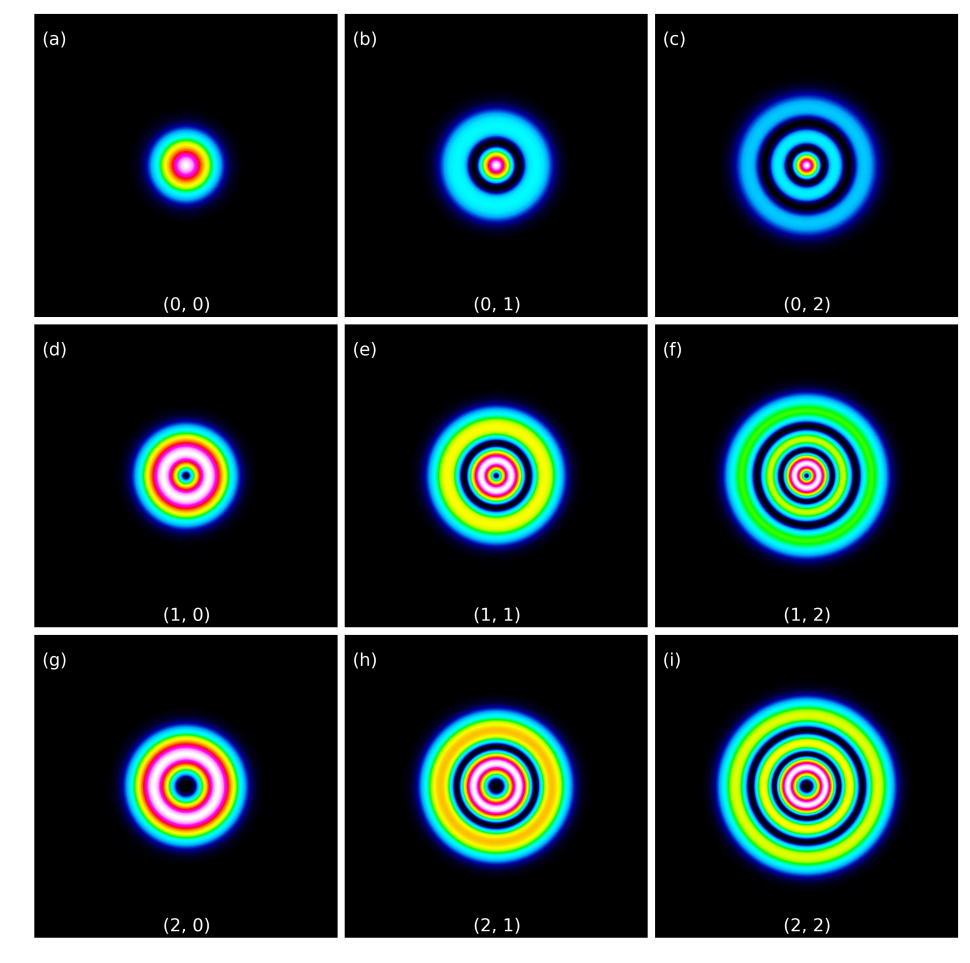
When the wave equation is solved with polar coordinates, the Laguerre-Gaussian modes are found. The Laguerre-Gaussian name comes from the associated Laguerre polynomial in the expression for the electric field. The associated Laguerre polynomial is described by n and k where k=n=0 is again the fundamental mode, TEM\(_{00}\). Only for the fundamental mode is the equation for the Hermite-Gaussian mode and the Laguerre-Gaussian mode equal. We have included images of various Hermite-Gaussian (see Figure 1) and Laguerre-Gaussian beams (see Figure 2).
Multi-mode beams and M²
Since the fundamental mode has unique propagation properties and can be focused tightly in comparison to other modes, lasers are often designed to output only the fundamental mode. However, imperfections in the laser’s resonator cavity can cause beam distortions and the appearance of higher-order transverse modes (Paschotta 2006). M² provides an excellent metric to compare the quality of a real beam to that of a theoretical, fundamental beam. M² for a Hermite-Gaussian multi-mode beam is given by
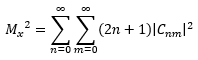
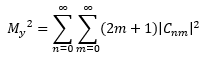
(Siegmann 1998). Where Cnm is a weighting factor for each of the TEMnm modes’ electric fields and together are represented by
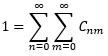
Using these three equations, we can calculate the theoretical M² of any laser beam whose modal composition and weights are known. DataRay has written software to generate theoretical beams, based on the Hermite-Gaussian and Laguerre-Gaussian equations. To validate our M² software algorithms, we compare the M² values generated from our software to the theoretical M² values. We find excellent agreement between the theoretical M² values and the software generated M² values for both single-mode and multi-mode beams. We generated a multi-mode Hermite-Gaussian beam comprised of TEM\(_{00}\), TEM11, and TEM22 modes with 50%, 25% and 25% weights respectively (see Fig. 3). The theoretical M² value based on the above equations is 2.5 for both the x and y axes. DataRay software returns a value of 2.52 for the x axis and 2.51 for the y axis. Both the x and y axes have a percent error less than one, therefore confirming the accuracy of the DataRay software.
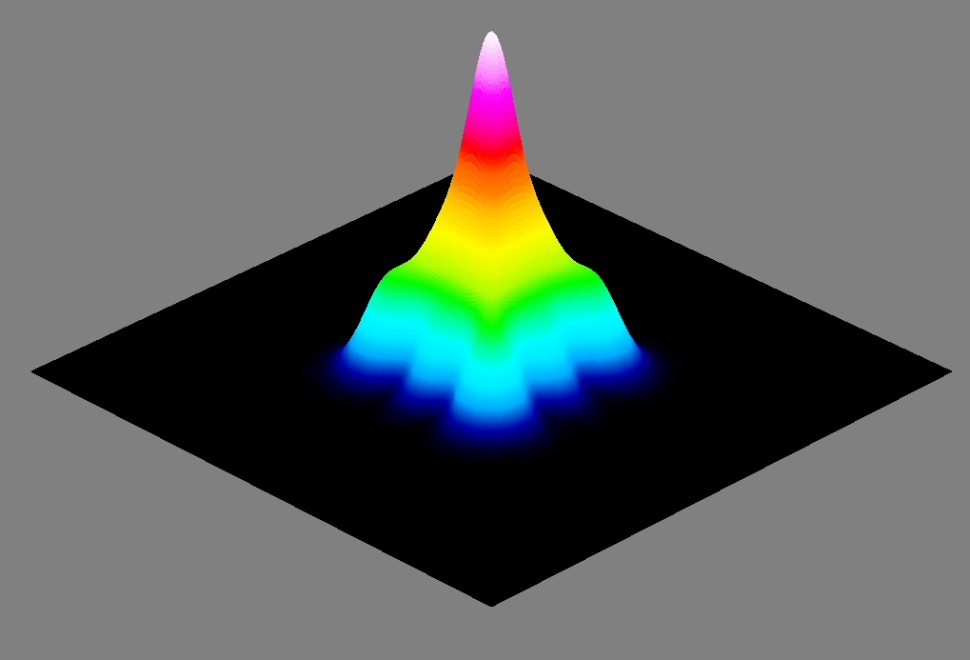
Similar to the Hermite-Gaussian modes, the theoretical M² value for a superimposition of various Laguerre-Gaussian modes can be found (Siegmann 1998). The M² value is defined as
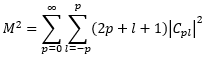
Where Cpl is the weighting factor for the various modes’ electric fields and is given as
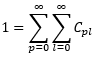
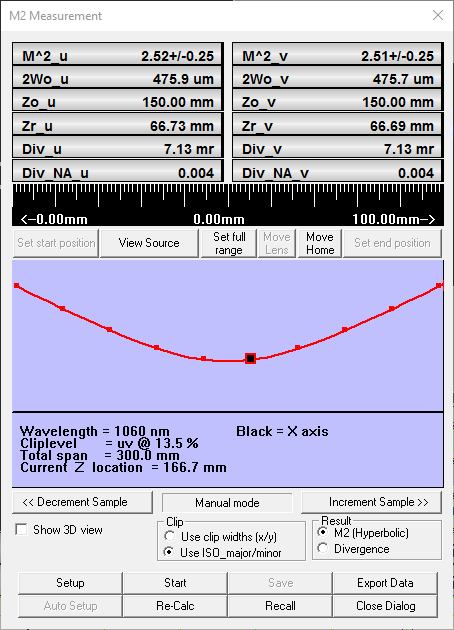
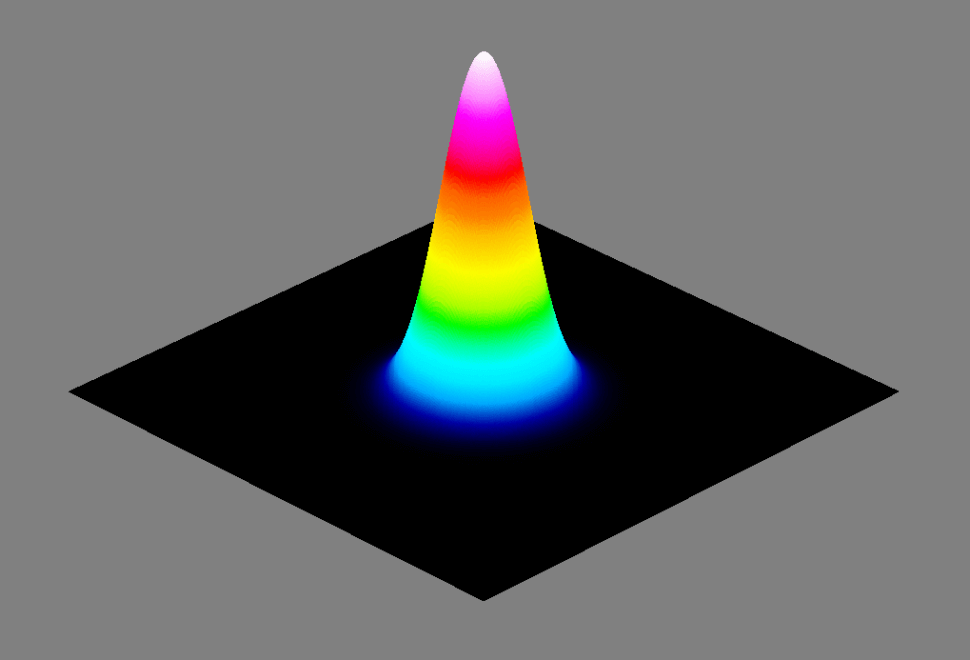
Once again, we generated a multi-mode beam; however, this beam consisted of Laguerre-Gaussian modes. The beam was comprised of 50% TEM\(_{00}\), 20% TEM\(_{11}\), and 30% TEM\(_{22}\) (Fig. 5). The theoretical value is calculated to be 3.4, and DataRay’s software returns a value of 3.41 (see Fig. 6). Once again, the percent error is less than one percent.


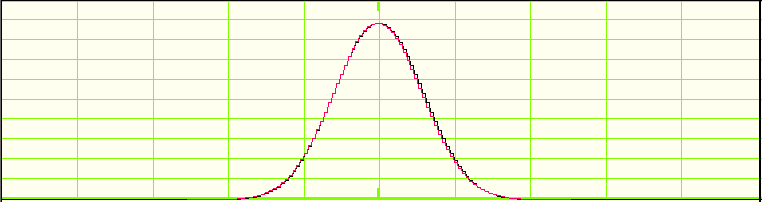
The previous two examples were somewhat exaggerated to demonstrate the effect of multiple modes in one beam. Often, the higher-order modes comprise a smaller percentage of the total beam intensity (see Fig. 7). Although these beams look Gaussian and have a close Gaussian fit (see Fig. 8), the superimposed high-order modes cause the M² value to deviate slightly from 1. Herein lies the importance of the M² measurement. Even though the multi-mode beam composition is not readily apparent through visual inspection of the beam, the M² value can accurately determine the beam quality. In the example shown (see Fig. 7), the Hermite-Gaussian beam is composed of 80% TEM\(_{00}\), 10% TEM\(_{10}\), and 10% TEM\(_{01}\). The theoretical M² value is 1.2 and DataRay’s software also returns a value of 1.2.
Conclusion
We have discussed the various Hermite-Gaussian and Laguerre-Gaussian higher-order transverse modes, as well as their effect on the M² measurements. In calculating the M² value of different modes, DataRay’s software returns a M² value within one percent of the theoretical M² value. DataRay offers a variety of beam profiling cameras and scanning slit beam profilers with stages to take accurate M² measurements. Additionally, DataRay’s patented BeamMap2 takes instantaneous measurements for quick beam quality determination. If you have any questions regarding either M² measurements or multi-mode beams, please contact us.
References
Author: Lucas Hofer
Products Mentioned

BeamMap2
- Robust, multi-plane beam profiling
- Real-time M², divergence, pointing, and focal measurements
Related News
M² Measurement
M Squared |April 12, 2016
As leaders in the laser beam profiling business, we have worked with M² for decades. In this blog post we discuss M², when to use it, and the way it is measured.

